Testando o cristal da placa mãe
Quando publiquei aqui no blog a parte 2 do artigo Frequencímetro com PIC de 1Hz a 50MHz o leitor Jackson Fadler colocou o seguinte comentário:
“Olá Paulo. comprei um deste apenas para teste do cristal, mas o único que ele não mede: é aquele cilíndrico de 32,789KHz das placas de PCs. Troquei um bocado desses cristais pensando que tinha defeito e não tinha. O que eu preciso saber que não sei sobre o teste dele?”
Adoro quando os leitores fazem comentários, primeiro porque é sinal que leram, mas principalmente quando exigem um desdobramento do assunto tratado.
Naquele momento respondi-lhe que iria catar alguns destes cristais por aqui e verificar o que estava acontecendo.
Eu não trabalho com placa mãe e, portanto não havia me lembrado destes cristais cuja frequência correta é 32,768kHz e já veremos por quê.
Lembrei-me que estes cristais são usados também em relógios e cronômetros digitais com display de cristal líquido similares ao que que vemos na fig.1.

Fig.1 – Relógio com cristal de 32,768kHz
Encontrei uns três deles por aqui nas minhas sucatas e testei os tais “cristais cilíndricos” no frequencímetro descrito no artigo e constatei que a dificuldade encontrada pelo leitor procedia.
Era hora de iniciar uma investigação sobre o assunto, pois como eu acredito na ciência, para mim, tudo o que se refere à tecnologia, em particular, tem que ter uma explicação plausível e cientifica. O resto é “achismo”!
O número “cabalístico” 32,768kHz
Seja nas placas mãe de computadores ou nos relógios, a função deste cristal é produzir a base de tempo de 1 segundo, para o RTC (Real Time Clock).
Mas, de qual “cartola” saiu este coelho, ou melhor, estes “32768 coelhos”?
Comecemos por lembrar que sistemas digitais são baseados em números binários, ou seja, com base 2 e não com a base 10 que nós humanos usamos na contagens e nas operações aritméticas do dia a dia.
Acompanhe na tabela abaixo o resultado de sucessivas divisões de 32768 por 2.
![]()
Observou que após 15 divisões sucessivas por 2 chega-se ao número 1, ou seja, 1Hz que corresponde ao período de 1 segundo como desejado para nossa base de tempo?
Estas 15 divisões podem ser obtidas facilmente com uma cadeia 15 Flip Flops tipo T o que torna a escolha desta frequência bastante interessante.
Agora que já encontramos a “cartola” e seus 32768 “coelhos” podemos prosseguir com a análise do problema.
Cristais ou ressonadores
De maneira bem resumida, podemos dizer que alguns materiais como o quartzo, por exemplo, produzem uma ddp quando sofrem alguma deformação em sua estrutura por causas mecânicas ou também podem produzir a deformação quando uma ddp lhes é aplicada e tal “deformação” ocorre em frequências determinadas pela maneira como cristal é cortado.
Basicamente existem duas maneiras de fabricar componentes, a partir de um cristal de quartzo a serem usados como referência de frequência em osciladores:
1) Cortando o cristal de forma a vibrarem numa frequência específica quando excitados por uma ddp.

Por dentro do cristal cilíndrico
2) Construindo uma lâmina a partir do cristal na forma de um “garfo” daí a denominação tuning fork cuja tradução ao pé da letra seria “garfo de sintonia”.
Em português a expressão tuning fork costuma de receber a designação de diapasão.
Na fig.2 temos um exemplo destes diapasões que lembram os dentes de um garfo.

Fig.2 – Diapasão
Ao tocarmos com algum objeto num dos “dentes” do garfo a estrutura vibrará num determinada frequência que dependerá do tamanho do “dente” do garfo.
Na fig. 3 temos, a guisa de curiosidade, um kit com 8 peças que vibram nas seguintes frequências:
C’ = 256Hz, d’ = 288Hz, e’ = 320Hz, f’ = 3411/3Hz, g’ = 384Hz, a’ = 4262/3Hz, b’ = 480Hz e c” = 512Hz.

Fig. 3 – Kit com 7 diapasões
Voltando aos “nossos cristais” usados em osciladores, a segunda opção, ou seja, os tuning forks, são mais baratos para construír e funcionam com boa acurácia para frequências da ordem de quilohertz e por isso, têm sido escolhidos para a fabricação dos cristais de 32768Hz usados para obter a base de tempo de 1 segundo.
Por que o frequencímetro não funcionou?
Depois de pesquisar muito na Internet e ler alguns papers de vários fabricantes sobre o tal “cristal cilíndrico” usado em relógios e placas mãe de computador eu comecei a vislumbrar uma resposta “técnica” para o leitor: – este tipo de cristal, aparentemente, talvez não fornecesse energia suficiente para excitar o oscilador usado no frequencímetro para testar cristais cujo esquema eu reproduzo na fig. 4.
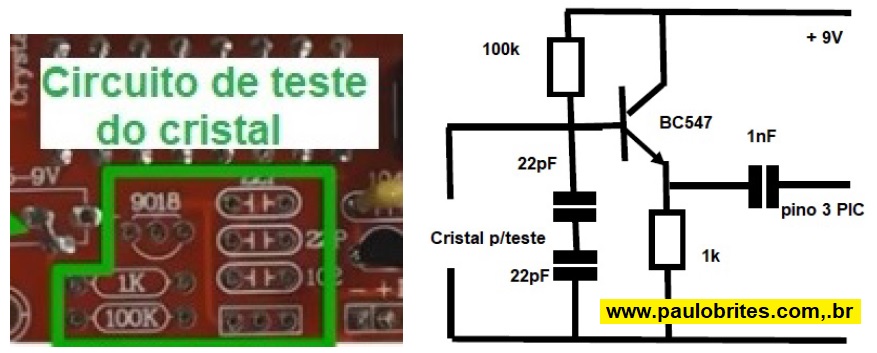
Fig. 4 – Circuito de teste de cristal
Esta era ainda uma suspeita, logo precisava ser melhor investigada.
Continuando as buscas na Internet encontrei um artigo de Mr. Albert van Bemmelen que endossava minhas suspeitas e sugeria um circuito relativamente simples para testar este tipo de cristal.
O circuito integrado CD 4060
A solução proposta por Mr.Bemmelen utiliza o CD4060 que é um oscilador e contador/divisor de frequência de 14 estágios que eu já conhecia desde os meus tempos de estudante auto didata de eletrônica digital pelos idos de 1980.
Vamos dar uma olhada na fig. 5 e ver como este CI funciona antes de partir para a minha versão do testador inspirada na sugestão de Mr. Bemmelen.
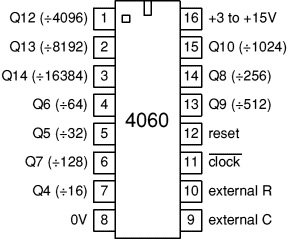
Fig. 5 – Pinagem do CD4060
Os pinos 10 e 11 recebem o CLOCK que no nosso caso será produzido pelo cristal de 32,768kHz que queremos testar.
Internamente o CI produz 10 divisões de frequência nos pinos 1 a 7 e 13 a 15.
No circuito que eu vou propor a seguir utilizaremos os pinos 1, 2 ou 3 que nos fornecerão frequência de 8Hz, 4Hz e 2Hz respectivamente e mais adiante você entenderá por que escolhi estas três frequências
De acordo com o data sheet do CD4060 devemos manter o pino de RESET (12) em nível baixo para não desabilitar o oscilador.
Sendo assim, este pino será ligado ao negativo (ground) da fonte junto com o pino 8.
A alimentação é feita no pino 16 e pode variar de 3V a 15V o que torna nosso circuito bastante versátil, entretanto aqui vale uma observação, na prática o circuito não funcionou com alimentação abaixo de 6V.
Eu levanto duas hipóteses:
1) a corrente consumida pelo LED, embora baixa, pode ter afetado o funcionamento do CI.
2) Já tive problemas no passado ao tentar alimentar CMOS de alguns fabricantes com 5V.
Algo a ser investigado, por isso optei por 9V que dá até para usar com bateria.
O JIG de teste para cristal de 32,768kHz
Na Fig. 6 temos a versão do testador que eu fiz.
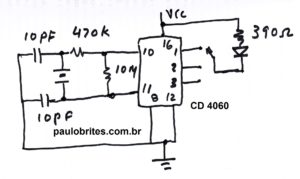
Fig.6 – Jig de teste para cristal 32768Z com CD4060
Para facilitar a vida do técnico eu optei por usa um LED ligado entre o positivo da fonte através de um resistor limitador de corrente (390ohms) e os pinos 1, 2 ou 3.
Por que escolhi estes pinos?
Muito simples, se você voltar a Fig. 6 verá que nestes pinos obteremos as frequências 8Hz, 4Hz e 2Hz que correspondem aos períodos de 0,125s, 0,25s e 0,5s respectivamente fazendo com que o LED pisque nestes intervalos de tempo facilmente observáveis visualmente.
Frequências maiores, portanto com períodos menores começam a se tornarem difíceis de visualização por causa da nossa persistência de visão.
#Partiu montagem
Primeiro fiz alguns ensaios numa protoboard para ver se tudo funcionava a contento e posteriormente resolvi montar tudo numa pequena placa padronizada de circuito impresso como vemos na Fig.7.

Fig.7 -Montagem do JIG para teste cristal de placa mãe
De volta ao frequencímetro
Quando eu já ia encerrando o artigo me surgiu uma ideia: – e se eu injetasse uma das saídas do 4060 no frequencímetro?
Pois bem fiz isso e funcionou o que parece demonstrar alguma incompatibilidade do cristal com o circuito oscilador proposto no frequencímetro mostrado na figura 4.
Futuramente pretendo investigar mais isso.
Por ora temos uma solução simples e barata para testar o cristal de 32,768kHz que atende inclusive a quem não possui o frequencímetro nem osciloscópio.




23 Comentários