Fazendo contas de cabeça
Fazendo contas de cabeça
 A matemática é uma das disciplinas, que a civilização nos põe como obrigatória de ser estudada, que aparece quase como unanimidade, entre os estudantes, como uma das mais difíceis.
A matemática é uma das disciplinas, que a civilização nos põe como obrigatória de ser estudada, que aparece quase como unanimidade, entre os estudantes, como uma das mais difíceis.
Ela parece estar no rol daquelas coisas que se ama ou se odeia. Na melhor das hipóteses, se suporta porque não tem outro jeito.
Eu particularmente nunca tive grandes problemas com ela e em particular “fazendo contas de cabeça” até hoje.
Sempre que digo que (entre outras coisas) sou professor de matemática, escuto um sonoro “chiiiiiiiiiiiiii”.
Agora, aposentado, voltei a dar aulas particulares para uma faixa etária com a qual não nunca tinha trabalhado antes, crianças e pré-adolescentes, pois desde sempre lecionei para jovens e adultos, público que, em particular, eu adoro.
E nesta minha nova experiência de vida notei uma coisa que, embora não seja novidade para ninguém, me fez pensar no assunto e escrever sobre ele: ver as crianças contando pelos dedos na hora de fazer uma conta de somar ou subtrair.
Sinceramente eu não consigo me lembrar de eu mesmo usar este “recurso” quando era criança, embora já lá se vão muitos anos.
Sou de uma geração em que éramos obrigados a decorar a tabuada o que para muitos era o maior terror.
Posso até concordar que alguns exageros eram cometidos e para tentar corrigi-los “novas didáticas” foram sendo criadas e usadas.
Fato é que quando as crianças de hoje têm que somar, por exemplo, 9 + 7, a maioria não consegue responder automaticamente 16 e precisam recorrer aos dedos e mesmo assim, muitas vezes, acabam dando a resposta errada.
Em principio, nada contra a esta prática, mas agora pense na seguinte situação caso você seja motorista amador ou profissional: você para pra pensar quando precisa mudar de marcha, por exemplo?
O que eu estou querendo dizer é que existem coisas nas nossas atividades diárias que precisamos realizar automaticamente e eu incluiria aí, entre elas, as contas de somar e subtrair, como uma das mais relevantes.
Então, alguém poderia me perguntar, você está defendendo a “decoreba” da tabuada?
Vou responder usando o método socrático, com outra pergunta:
– por acaso para aprender a ler e escrever você não teve que decorar o alfabeto, a associação dos sons a grafia das letras, bem como a combinação delas?
Então porque a bronca em decorar, pelo menos, a tabuada de adição?
Uma vez o aluno sabendo de cor como fazer uma adição, sem ter que ficar contando pelos dedos, ele pode ser conduzido a pensar a subtração como uma operação inversa (sem que este “nome” seja usado num primeiro momento).
E aqui eu gostaria de parar por um momento esta discussão para tratar um pouco sobre questões relativas ao funcionamento do nosso cérebro.
E o que você diria se eu disse que o nosso cérebro é preguiçoso e não foi projetado para pensar?
Levou um susto com esta afirmação, pois quem afirma isto não sou eu e sim, os neurocientistas.
Aqui abro um parêntese para recomendar um livro bastante interessante de Daniel Willingham: Por que os alunos não gostam da escola?
Nele o autor cita uma declaração de Henry Ford: “pensar é a tarefa mais difícil que existe, razão provável pela qual poucas pessoas se ocupam em fazê-lo”.
E aqui o pensar significa resolver problemas, raciocinar, realizar um trabalho mental que exija algum esforço.
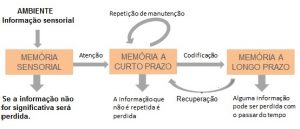
O pequeno diagrama acima pode nos ajudar a entender como nosso cérebro “trabalha”.
O cérebro recebe a informação do ambiente, pode ser uma imagem, um som ou uma emoção. Se a informação não for significativa ela, provavelmente, será perdida.
A seguir esta informação vai para uma área do cérebro chamada de memória de curto prazo (MCP). Ela precisa ser trabalhada (codificada) para passar para memória de longo prazo (MLP), entretanto se ela não for praticada (repetida) ela será perdida.
Está percebendo onde estou querendo chegar com a questão de decorar a tabuada?
Mas há uma questão a ser analisada ainda. Para que a informação chegue a MCP ela precisa ser significativa.
Em outras palavras o aluno precisa julgar e acreditar que a informação que estamos fornecendo é relevante para ele e aí o papel do professor será importantíssimo para descobrir como tornar cada informação significativa para cada aluno.
Repare no bloco em vermelho que diz “a informação que não é repetida é perdida” a qual eu acrescentaria que após o primeiro estágio de ajudar o aluno a memorizar a tabuada a mesma precisa ser praticada (eu prefiro dizer praticar no lugar de dizer fazer exercícios), ou seja, temos que colocar o aluno para fazer milhões de “continhas de adição” (milhões mesmo) até que o processo se torne automático.
Ainda me lembro como a minha primeira professora, D.Maria no Colégio Senador Correia (naquela época não chamávamos a professora de tia!).
Usávamos caderno quadriculado para as aulas de matemática. Ela ocupava duas linhas inteiras com números que deveriam ser somados. Dava um susto danado ver aqueles “numerões” enormes para serem somados, mas quem aprendia, aprendia mesmo, para o resto da vida.
Após a “seção nostalgia” voltemos ao funcionamento do cérebro.
Uma vez que você aprende algo novo, já temos competência no assunto, mas a competência precisa ser transformada em habilidade e esta última só se adquire com a prática.
Ao receber a licença para dirigir um veículo uma pessoa está apta a fazê-lo, ou seja, supõe-se que tem competência para dirigir, mas só com o tempo ela saberá como reagir às situações que encontrará no dia-a-dia quando estiver ao volante e as informações que ela recebeu da memoria sensorial e terão que ser trazidas num piscar de olhos da MLP para a MCP, que é o pensamento e a consciência se realiza.
A habilidade em encontrar automaticamente o resultado de uma adição ou subtração sem ter que parar, pensar e contar pelos dedos tem que ser praticada, pois a informação que não é praticada é perdida. Esta habilidade será o diferencial para o aluno quando ele tiver que resolver exercícios em que uma operação matemática deste nível deve ser para ele como para um motorista é mudar de marcha ou pisar no freio na hora certa.
Uma vez que a adição (e por consequência a subtração) já estão incorporadas ao processo mental e o aluno responde que 9 + 6 é igual a 15 sem “pensar” ele pode passar a trabalhar a multiplicação.
Neste momento já se pode explorar um pouco mais cognitivamente e mostrar que a multiplicação nada mais é uma adição disfarçada.
Entretanto, novamente a tabuada de “vezes” precisa ser “aplicada na veia” e para o aprendiz 8 x 7 = 56, por exemplo, é a mesma coisa que comer um chocolate. Alguém para pra pensar antes de comer um chocolate? (se parar pra pensar não come com medo de engordar!).
Novamente a prática é que vai desenvolver a habilidade e aí as multiplicações de números imensos se encarregarão de fazer a “musculação” do cérebro.
Nesta primeira fase do aprendizado eu defendo a ideia que ninguém precisa saber como funciona o aparelho digestório para almoçar e jantar.
O que eu estou querendo dizer é que não acho que seja a hora de tentar justificar o que há por trás de uma operação de adição ou multiplicação com as chamadas propriedades comutativas e distributivas.
Certamente o aluno nesta idade nem sabe bem o significado destas palavras e por não entendê-las começa a achar que matemática é difícil.
Não é a matemática que é difícil e sim o português (se esta for a sua língua materna)!
O professor precisa ser extremamente cuidadoso com as palavras que usa em sala de aula e ter clareza que para os ouvintes (alunos) significam o que ele está pretendo dizer.
Quando eu lecionava física para jovens e adultos e ia começar a tratar de unidades de medidas, distribuía para eles o texto de Sergio Porto (Stanislaw Ponte Preta) “Medidas, no espaço e no tempo” e pedia que eles fizessem uma leitura “licenciosa” e fossem marcando as palavras que não conheciam.
Depois eu anotava no quadro aquelas palavras e via se a dúvida era comum a todos ou apenas a um ou outro aluno.
Quando a dúvida se instalava de um modo generalizado eles eram convidados a procurar o significado no dicionário (que eu levava para a sala de aula).
Não dá para tentar ensinar nada a ninguém se você fala grego e a sua plateia só entende japonês!
Pense nisso e até sempre.






10 Comentários