Você sabe qual a diferença entre valor RMS e True RMS?
Você sabe qual a diferença entre valor RMS e True RMS?
Para entender qual a diferença entre valor RMS e True RMS parece óbvio que é preciso que você entenda primeiro o que é valor RMS.
O termo “true” significa verdadeiro, então será existe um RMS de mentirinha e outro “verdadeiro”, é isso?
A sigla RMS significa Root Mean Square que “em bom português” quer dizer Raiz Média Quadrática também denominado de Valor Eficaz.
Hum! Isto está cheirando a matemática! Então, vamos a ela, sem medo de ser feliz.
Antes de tudo que tal destrincharmos cada uma destas palavras separadamente para tentar entender o que significam juntas.
Comecemos com “raiz” e “quadrática”.
Por exemplo, dois elevado ao quadrado é igual quatro (22 = 4). Encontrar ou “extrair a raiz quadrada de 4” é descobrir qual o número que elevado ao quadrado dá 4 que neste exemplo nós sabemos que é 2.
Então qual é a raiz quadrada de 25? Ora, é o número que elevado ao quadrado dá 25 e “o prêmio vai para…. o número 5”.
Depois desta breve revisão sobre raiz quadrada, para acordar seus neurônios dorminhocos, falemos das médias (que neste caso não é de café com leite).
Em matemática podemos calcular diversos tipos de média e mais comum de todas é a média aritmética que embora não seja de interesse em nosso “estudo” sobre RMS irei abordá-la não só como curiosidade, mas também para ajudar a compreender o que vem pela frente.
Média aritmética: uma revisão rápida
Suponhamos que numa determinada escola para o aluno passar de ano tenha que obter média aritmética 7 em quatro avaliações. Assim, ele terá que somar 28 pontos nas quatro avaliações porque 28 dividido por 4 é igual a 7, logo se ele tirou 4 na primeira prova, 6 na segunda, 9 na terceira até aqui só somou 19 pontos, então ele vai ter que se virar para tirar 9 na quarta avaliação.
Vai ter que estudar muito (se precisar de aula particular fala comigo kkkk)!
E a média quadrática, como é que fica?
Esta é um pouquinho mais sofisticada e menos usada no dia-a-dia, mas muito importante quando falamos de tensões e correntes alternadas que é o nosso caso.
Por definição
Parece confuso, mas não é. Vamos a um exemplo numérico.
Usando as notas do aluno vadio teremos primeiro que fazer a média aritmética dos quadrados dos quatro números, ou seja, (42+62+92+92)/4= 214/4 = 53,5.
Se quiséssemos achar a Raiz Média Quadrática teríamos que extrair a raiz quadrada de 53,5 que dá aproximadamente 7,314 (a conta foi feita com calculadora).
Mas qual seria o interesse de se extrair a raiz da média quadrática?
No caso das notas nenhum, mas na medida de tensões e correntes alternadas é muito importante, como veremos.
Deixemos este assunto das médias temporariamente de lado e passemos a algumas considerações sobre a nossa corrente/tensão alternada.
Como medir uma tensão ou corrente alternada?
Medir uma corrente ou tensão alternada não é uma tarefa fácil uma vez que seus valores variam continuamente ao longo do tempo e um instrumento analógico (aquele de ponteiro) não conseguiria acompanhar estas variações.
Nosso estudo se prenderá, inicialmente, as formas de onda senoidais que são as da tensão das nossas tomadas e por isso, nos interessam mais.
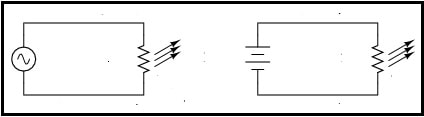
Já que não se tinha uma maneira fácil de medir todos os valores de uma tensão alternada (senoidal, por exemplo) alguém teve a ideia de fazer a comparação entre o efeito térmico que uma corrente contínua e uma alternada senoidal pura apresentaria quando aplicadas (uma de cada vez, é claro) a uma carga resistiva.
A experiência
Suponhamos a seguinte experiência.
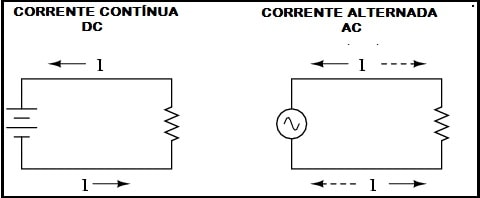
Alimentamos uma resistência R de 100Ω com uma tensão continua igual a 200V durante 1 hora, por exemplo.
Pela Lei de Ohm sabemos que a corrente no circuito será 2A e a potência P dissipada que é dada em watts será calculada por P = RxI2 = 100×22 = 400W.
Aqui surge uma dúvida, e se em vez de uma corrente continua aplicássemos uma alternada qual valor que deveríamos usar para obter a mesma temperatura, ou dissipar os mesmos 400W, depois do mesmo tempo?
Seria 100V também? Mas que “100V” é este, o valor de pico da senóide?
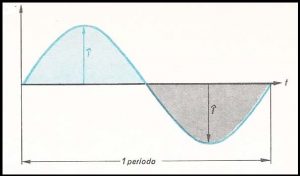
Ocorre que este valor de pico, tanto positivo como negativo, só está presente duas vezes em cada ciclo.
Poderíamos então pensar num valor que correspondesse a uma média aritmética dos valores da senóide.
Mas esta média daria zero já que a média aritmética do semiciclo negativo anularia a média do semiciclo positivo.
Usamos então um artifício. Fazemos uma retificação de meia onda, calcularmos a média aritmética do semiciclo positivo e depois multiplicamos o resultado por dois.
Em outras palavras, uma retificação de onda completa.
O valor médio de uma senóide retificada em meia onda
Comecemos calculando o valor médio de uma senóide retificada em meia onda.
Par encontrar o valor médio, neste caso, também chamado de valor DC, precisaremos somar todos os valores de tensão do semiciclo e dividir pela quantidade de valores.
Usando um pouquinho a sua imaginação você concluirá que ao somar todos os valores de tensão neste semiciclo da senóide você estará calculando a área sob o semiciclo da senóide.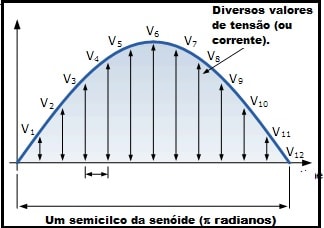
O cálculo desta área exige o uso de uma “ferramenta” matemática chamada cálculo diferencial e integral que não será feito aqui para não correr o risco de fazê-lo abandonar a leitura, mas juro, por tudo que há de mais sagrado, que esta área dá um valor igual 2 vezes Vpico.
Agora precisamos dividir esta área pelo número de valores que vai de 0 até 2Π, ou seja, um ciclo completo.
Esta continha nos dará o valor médio do semiciclo da senóide.
Vamos a ela: 2Vpico/2π= 1/π Vpico = 0,318 Vpico.
Você não precisa lembrar-se destas contas, mas não pode esquecer-se do resultado final.
Agora fica fácil concluir que o valor médio de uma retificação de onda completa será o dobro deste valor.
O que nós estávamos querendo saber mesmo?
Depois de todas estas contas e explicações é possível que você já nem lembre mais o que estávamos querendo saber.
Vou reativar sua memória: nós queríamos saber se o valor médio de uma senóide (completa) produziria a mesma potência que uma tensão continua.
Vamos fazer as contas e chegar a conclusão (que não).
Na nossa experiência vimos que para 200VDC em 100Ω obtivemos P = 400W.
Se a senóide tiver um valor de pico também de 200V obteremos uma corrente média igual a
I = 0,636×200/100 = 1,272A o que dará P = 100 x (1,272)2 = 161,79W, ou seja, um valor bem menor que 400W.
Daí pode-se concluir que para obter a mesma potência precisaremos ter uma senóide com valor de pico bem maior. Mas quanto será este valor “bem maior”?
E assim nasceu o valor RMS
Que tal experimentarmos a média quadrática em vez da média aritmética?
Para fazer a média quadrática precisamos primeiro elevar a nossa “querida” senóide ao quadrado e depois de fazer a média aritmética destes valores extrair a raiz quadrada do resultado.
Novamente vou ter que jurar que ao fazer estas contas encontraremos o valor mostrado a seguir.
Se você não confia em mim e quiser ver todas as contas tim por tim então clique neste link e seja feliz.
Entretanto, é preciso que fique bem claro que estes, fatores (0,7 e 1,41) só valem para senóides “bem comportadas”, aquelas que, em geral, só existem nas páginas dos livros.
Como “enganar” um voltímetro analógico
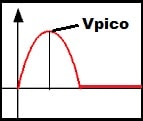
Como eu disse no início o voltímetro analógico não tem como medir a tensão RMS, o que podemos fazer é uma retificação de onda completa e medir o valor médio.
(Abra o seu analógico e você encontrará os dois diodos lá dentro numa configuração parecida com a da figura abaixo).
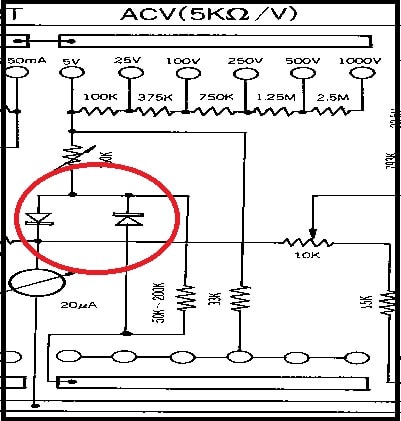
Circuito para medir tensão AC em multímetro analógico
Nunca é demais lembrar que valor médio e valor RMS são diferentes, mas podemos relacionar os dois da seguinte maneira:
Vmédio = 0,636 Vpico ou Vpico = Vmédio/0,636
VRMS = 0,7 Vpico ou Vpico = VRMS/0,7
Logo Vmédio/0,636 = VRMS/0,7 ou
VRMS = (0,7/0,636) Vmédio =1,11 Vmédio.
Então, o voltímetro na verdade o analógico mede o valor médio de uma senóide retificada em onda completa, mas o painel é calibrado com uma escala 1,1 vezes maior que o valor medido, ou seja, é um valor RMS “de mentirinha”.
Esta mentirinha é quase uma verdade se a senóide for bem “bonitinha”, isto é, sem harmônicos.
A relação entre o valor RMS e o valor médio é denominada FATOR DE FORMA e pode ser muito útil para determinarmos o valor RMS para outras formas de ondas “bem comportadas” e que não sejam senoidais, tais como ondas triangulares ou quadradas. No caso particular da senóide o fator de forma é 1,11 como acabamos de calcular. Voltaremos a isto mais a frente.
Finalmente o TRUE-RMS
Com a chegada dos voltímetros digitais e com chips conversores A/D capazes de tomar um grande número de amostragens, bem como incluindo algoritmos matemáticos poderosos para fazer aquelas contas do cálculo diferencial e integral tornou-se possível fabricar multímetros capazes de medir ondas mesmo não senoidais puras e expressar no display o valor “verdadeiro” da tensão RMS.
Por que é importante o True-RMS
Para o técnico de eletrônica não é muito importante, em geral, a diferença apresentada por um voltímetro RMS “de mentirinha” e um TRUE-RMS, entretanto para o eletricista a diferença de leituras pode ser crucial para identificar defeitos “estranhos” numa rede elétrica provocados por harmônicos oriundos de cargas reativas ou dispositivos eletrônicos com SCR ou TRIAC.
Portanto, se você é eletricista (ou pretende ser) e vai comprar um amperímetro alicate a melhor opção é, sem dúvida, um modelo TRUE-RMS.
O valor RMS de uma onda triangular
O cálculo da tensão RMS não se aplica apenas a tensões e correntes senoidais, embora isto seja o mais comum.
Há que se ficar atento, entretanto para o fato de que o fator 1,41 (conhecido como fator de crista) apresentado acima aplica-se exclusivamente a ondas senoidais puras.
Suponhamos que queiramos calcular o valor RMS de uma onda triangular como a mostrada abaixo.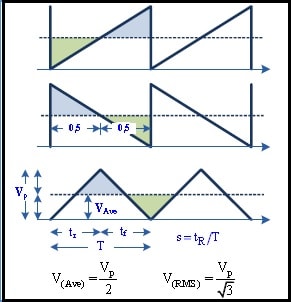
Mais uma vez não apresentarei os cálculos, pelas razões já expostas, entretanto o que importa é você saber que no caso de uma onda triangular periódica o valor RMS será obtido multiplicando-se o valor de pico por 0,557 ou que o fator de forma neste caso é 1,154.
Fator de Crista e Fator de Forma
Finalmente talvez valha a pena encerrar este post com duas fórmulas que podem ser útil principalmente para quem está estudando para concursos.
E para arrematar aviso que os concurseiros de plantão devem memorizar a tabela abaixo e boa sorte.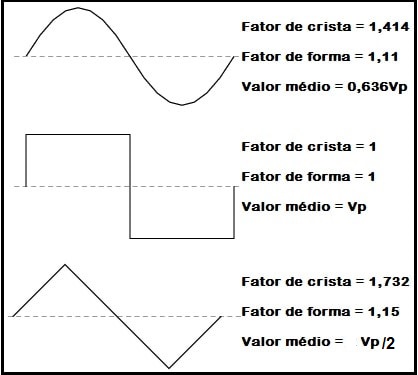
Quem estiver interessado na matemática avançada para o cálculo de RMS CLIQUE AQUI.
18 Comentários