Trigonometria na Eletricidade e na Eletrônica – Parte II
Trigonometria na Eletricidade e na Eletrônica – Parte II
Na primeira parte deste artigo eu tratei da trigonometria a partir de seus fundamentos que surgiu da ideia de associar ângulos a relações entre os lados de um triângulo retângulo dentro de uma circunferência através de uma tabela.
Naquele momento ainda não ficou claro como esta “ferramenta” matemática vai se relacionar com a Eletricidade e a Eletrônica como era a “promessa” do título. Pois bem, como não sou político nem candidato a nada vou cumprir a promessa agora na segunda parte do artigo.
Até, mais ou menos, o século XVI geometria e álgebra eram ramos da matemática que seguiam caminhos separados.
Só em 1639, ao publicar sua obra-prima, Discurso sobre o Método, foi que o francês René Descartes (leia-se decartes, o S é mudo) começou a juntar os dois ramos da matemática, geometria e álgebra, “inventando” a Geometria Analítica. As novas ideias de Descartes iriam produzir um efeito enorme no desenvolvimento da ciência.
Em linhas gerais a geometria analítica de Descartes permitiu que se representasse qualquer tipo de curva geométrica através de uma expressão algébrica, assim cada curva (ou reta) passaria a ter uma equação associada a ela.
A partir da analise da equação de uma reta ou curva pode-se tirar muitas conclusões.
A “sacada” de Descartes abriu o caminho, para mais tarde, Newton “inventar” o cálculo diferencial que revolucionaria toda a ciência.
No nosso caso específico da trigonometria, que estamos estudando, veremos que os valores do seno e do cosseno de cada ângulo poderão ser representados por uma curva mostrando suas variações. Estamos falando da senóide e da cossenóide que, você já deve estar percebendo que deve ter algum “parentesco” com a tensão ou a corrente alternada senoidal. Vejamos como.
Gerando uma “corrente” alternada senoidal
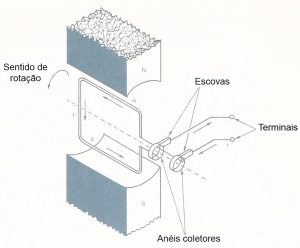
Como dizem os chineses “uma figura vale mais que mil palavras”, então vamos olhara para a figura 9 e tirar algumas conclusões.
Nesta figura temos uma espira de fio condutor que através de algum tipo de construção mecânica poderá girar imersa em um campo magnético fixo.
Este é o princípio básico que permite a geração de uma diferença de potencial nos terminais de uma bobina. A cada volta da espira um valor diferente de tensão aparece nos seus terminais que começa de zero volt quando a espira está na vertical, vai subindo de valor à medida que a espira gira até chegar a um valor máximo quando estiver na horizontal. Novamente começar a diminuir até retornar ao zero. Neste instante o processo começa a ocorrer inversamente. Sugiro que você click no link a abaixo para acompanhar o processo a partir do slide 6:
http://www.pbslearningmedia.org/asset/ate10_int_generation/
Vamos acompanhar também este processo pela figura 10 para entender como a trigonometria vai entrar nesta historia.
É aqui que a geometria ou a trigonometria vai se encontrar com a álgebra permitindo que se escreva o seno de um ângulo não apenas como a relação dos lados do triângulo retângulo, porém através de uma equação ou “função trigonométrica”.
Grosso modo, o que se chama de função em matemática é um “tipo” de equação com duas incógnitas, que no caso das funções são chamadas de variáveis, onde uma depende da outra ou, em outras palavras, é “função” da outra.
Os matemáticos chamam estas variáveis de x e y e escrevem y = f(x) que se lê “o valor de y é função (depende) do valor de x” ou sinteticamente: “y igual a f de x”.
No nosso caso a variável x será o tempo e, por isso prefere-se usar a letra t no lugar de x. Esta variável representará o tempo que a nossa bobina levará para dar uma volta completa dentro do campo magnético.
Este “tempo” pode ser especificado pelas unidades usuais de tempo como segundo ou minuto ou em graus que no caso da rotação da bobina costuma ser chamados de “grau elétrico” e que na figura 10 está representado pela letra grega Φ (fi) e está na linha horizontal ou “eixo” horizontal.
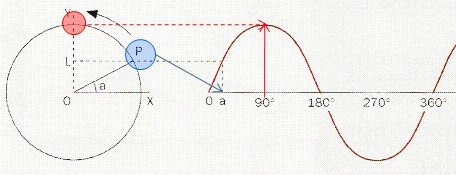
Agora observe que o segmento que vai do ponto A da circunferência até a linha horizontal no lado esquerdo da figura 10 é exatamente a meia corda que foi apresentada na parte I deste artigo e denominada por seno do ângulo Φ.
Se cada valor do seno for transportado para o gráfico à direita onde colocamos o eixo horizontal, obteremos uma curva que representa as variações da tensão “e” produzida pela bobina girando dentro do campo magnético.
Observe que a tensão “e” é uma função do valor do seno do ângulo Φ sendo que o valor máximo que ele pode assumir (Em ou Emax) está relacionado ao raio da circunferência e, assim podemos escrever e = Em sen Φ, de modo que para cada valor do ângulo Φ teremos um valor da tensão correspondente que vai de zero até um valor máximo (Em) ao chegar a 90º ou um quarto de volta. Deste ponto em diante começamos a ter os mesmos valores anteriores (entre 0º e 90º).
Um fato interessante nesta “nova” abordagem da trigonometria é que podemos calcular o seno de ângulos maiores que 90º o que não seria possível se ficasse restrito apenas a trabalhar com o triângulo retângulo.
Antes de prosseguirmos vale chamar a atenção para uma confusão que os estudantes costumam fazer. Os dois “morrinhos” que aparecem na figura 10, um virado para cima e outro para baixo, NÃO são semicircunferências.
Numa circunferência cada ponto da curva está a uma distância constante do centro que é o raio da circunferência, enquanto no gráfico da figura 10 a curva segue a variação do seno, por isso esta curva é chamada de senóide.
Outra maneira de olhar este problema – o movimento circular uniforme.
É fácil perceber que o ponto A da nossa figura 10, que, nosso caso, representa cada posição da bobina girando dentro do campo magnético, descreve um movimento circular e como a bobina deverá girar com uma velocidade constante os físicos denominam este movimento de MCU ou Movimento Circular Uniforme onde a palavra “uniforme” neste caso quer dizer “velocidade constante”.
Entretanto, no MCU podemos definir dois tipos de movimentos simultâneos: o movimento do ponto A propriamente dito e o movimento do ângulo Φ e, por conseguinte podemos calcular dois “tipos” de velocidades diferentes: a do ponto A que chamaremos de velocidade linear e a velocidade do ângulo Φ que será chamada de velocidade angular, aliás, nada mais pertinente que este nome.
A velocidade linear que representaremos pela letra “v” é calculada dividindo-se o “tamanho” da trajetória do ponto pelo tempo que ela leva para completar cada volta. No nosso caso a trajetória é a circunferência de raio R e, portanto valerá 2πR para uma volta completa.
Neste caso o tempo de uma volta completa (ou ciclo) costuma ser chamado de período e representado pela letra T maiúscula para diferenciar do tempo genérico para o qual se usa a letra t minúscula.
No fundo “tesinho e tesão” não deixam de ser tempo e por isso, em geral, medido em segundos (poderia ser minuto ou hora).
Período e frequência, qual a diferença?
Quem estuda Eletricidade e Eletrônica escuta muito o termo frequência e sabe que ela é expressa em hertz ou seus múltiplos como quilohertz, megahertz, ou gigahertz, mas o que ela significa exatamente?
Vamos começar falando do período (T) para chegar à frequência.
Embora eu já tenha falado do período em parágrafos anteriores vamos a uma definição formal:
Período (T) é o tempo necessário para a bobina (ou qualquer coisa que gire) completar uma volta ou um ciclo.
Já a frequência, que se representa por f minúsculo, nos dá o número de voltas ou ciclos completados em um segundo (sempre um segundo).
Assim, por exemplo, se o período (T) for 10 segundos, significa que são gastos 10 segundos para completar uma volta ou um ciclo completo, logo em um segundo teremos dados apenas um décimo de volta logo a frequência é 0,1 ciclos por segundo.
Antigamente a unidade de frequência era ciclos por segundo (c/s), porém lá pelos anos 60 resolveram passar a chamar “ciclos por segundo” de hertz que se simboliza por Hz.
 Do exemplo numérico acima podemos concluir facilmente que há uma relação matemática bem simples entre o período (T) e a frequência (f), isto é, a frequência é o inverso do período ou o período é o inverso da frequência.
Do exemplo numérico acima podemos concluir facilmente que há uma relação matemática bem simples entre o período (T) e a frequência (f), isto é, a frequência é o inverso do período ou o período é o inverso da frequência.
Voltando ao MCU
Mas porque fiz esta aparente digressão na minha linha de pensamento indo de alhos para bugalhos e acabei por cair nestas definições de velocidades, períodos e frequências?
A velocidade, como todos sabem, mede a relação entre o “espaço” percorrido durante a trajetória do móvel em relação ao tempo gasto para percorrê-la. Basta olhar para o velocímetro do carro e esta lá disfarçadamente a fórmula para calcular a velocidade: km/h que nos livros de física que tratam preliminarmente deste conceito costuma aparecer como v = s/t.
No nosso caso particular em que a trajetória é uma circunferência vamos preferir trabalhar com a variação do ângulo que representaremos pela letra grega fi (Φ), pois este será o mesmo qualquer seja o raio da circunferência e assim, de uma maneira similar como fizemos com a velocidade linear definiremos a velocidade angular que será representada pela letra grega ômega minúscula (ω) como ω = Φ/t e, portanto podemos escrever Φ = ω t.
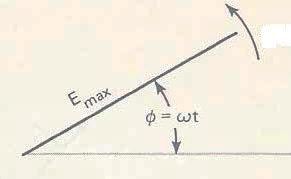
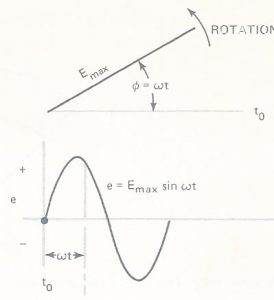
Voltando a figura 10 podemos reescrever a expressão
e = Emax sen Φ como e = Emax = sen ω t.
Você poderá argumentar, e com razão, que não é comum se usar a velocidade angular (ω) quando estamos trabalhando com Eletricidade e sim com a frequência (f).
Sem problemas. Como nossa trajetória é uma circunferência podemos escrever ω = 2π/T e como 1/T = f concluímos facilmente que a velocidade angular também pode ser escrita como ω = 2π f e então, a tensão senoidal pode aparecer na forma e = Emax sen (2π f)t .
E assim passamos a ter a expressão para uma tensão ou corrente ALTERNADA SENOIDAL em função da frequência. Veja a figura 12.
É bom você saber que os livros de Eletricidade preferem se referir à velocidade angular (ω) como frequência angular. Uma mera questão de palavras diferentes para dizer a mesma coisa.
Está percebendo como a trigonometria que nasceu lá na Grécia no século II aC com Hiparco se “infiltrou” na Eletricidade que nem sonhava existir naquela época. É a matemática descrevendo o Universo como disse Galileu.
Introduzindo o conceito de fase
A expressão algébrica para representar a senóide que vimos no parágrafo anterior partiu da ideia de que a rotação, que tanto poderia ser de uma bobina como uma roda de bicicleta, começou com o ângulo Φ = 0º.
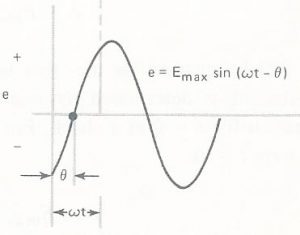
E o que aconteceria se o ângulo Φ fosse maior do que zero? Vamos chamar este ângulo de teta (Θ).
Neste caso diz-se que a senóide está “atrasada” e este ângulo teta é chamado, em Eletricidade, de ângulo de fase e será negativo para indicar o “atraso”.
A expressão algébrica da senóide passa a ser escrita como
e = Emax sen (ω t – Θ).
Veja a figura 13.
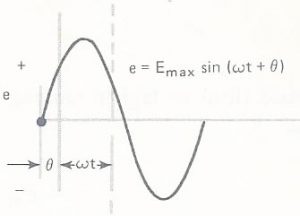
Na figura 14 temos a situação para uma senóide adiantada e, portanto teta será positivo e escreveremos:
e = Emax sen (ω t + Θ)
E o cosseno, também pode ser escrito assim?
Claro que sim porque o cosseno de um ângulo é igual ao seno de seu complemento como vimos na primeira parte deste artigo.
Em outras palavras, podemos dizer que o cosseno está adiantado de 90º em relação ao seno, o que nos permite e
e = Emax cos ω t = Emax sen (ω t + 90º)
Para que serve tudo isso ou resolvendo uma questão de concurso
Vejamos esta questão que caiu na prova para o cargo de tecnologista do Ministério de Ciência e Tecnologia em 2008.
A princípio você poderia estranhar que a questão menciona “sinal senoidal” e apresenta a expressão v(t) = 5 cos (ω t + 45º) mV.
Nada, porém há que estranhar porque seno e cosseno é praticamente a mesma coisa em termos de representação gráfica sendo que a única diferença entre as duas curvas será a defasagem de 90º.
Vou me aprender aqui a resolver apenas os itens 53 e 54 que são pertinentes ao que acabamos de ver neste artigo.
Considerando que f = 1kHz = 103 Hz, quando t = 125 µs = 125.10-6s teremos
v (125µs) = 5 cos (2π103 .125.10-6 + π/4)
A primeira coisa que o candidato precisa estar atento que tem que transformar 45º em π/4, pois temos sempre que trabalhar com radianos e não em graus.
Fazendo as contas dentro parênteses obteremos 5 cos (π/2) e, portanto v(125 µs) 0 mV o que torna a afirmativa verdadeira ao dizer que a amplitude do sinal é nula.
O item 53 é extremamente fácil. Lembre-se que o cosseno está adiantado 90º do seno, portanto podemos escrever
5 cos (ω t + 45º) = 5 sen (ω t + 45º + 90º) ou 5 sen (ω t + 135º) como propõe a questão.
Considerações Finais
O objetivo destes dois artigos foi mostrar com a trigonometria é importante na Eletricidade e que não é nenhum bicho de sete cabeças como muitos pensam.
Espero ter conseguido o meu objetivo.
Aguardo seus comentários.








4 Comentários